One of the most popular unsupervised learning models is Restricted Boltzmann Machines (RBM), which has been used for many types of data including images [Hinton06], speech representation [Mohamed11] and moving ratings [Salakhutdinov07] . It was another success in building a generative model for bags of words that represents documents [31], which indicate its potential capacity to build a model to predict the stock with financial documents. The most widely usage of RBM is composed to build a Deep Belief Network (DBN). The learning process of RBM is usually contrastive divergence. Experiences are needed to decide the setting of numerical parameters, such the batch size, the learning rate, the momentum, the number of epochs to iterate, the layers of hidden units, and how many units in each hidden layer, the update methods being deterministically or stochastically and the initialization of weights and bias. It also needs to be considered the way to monitor the learning process and stop criteria. This section will introduce the key components and training method of our DBN model, based on the guide in [Hinton10].
Restricted Boltzmann Machines
Energy based model assigns an energy value to each possible configuration of units by an energy function. The function will be trained to make it has some properties such as making the energy of desirable configuration has energy as low as possible. Boltzmann Machines (BMs) are a type of energy model in a form of Markov Ran- dom Field whose energy function is linear for its parameters. In order to make it sufficiently powerful to express complex functions, some invisible variables as hid- den units are added. The Restricted Boltzmann Machines is a restricted version of BMs, which constrain the BMs without the connections between different vision units or connections between di↵erent hidden units. A example graph is shown in figure below.
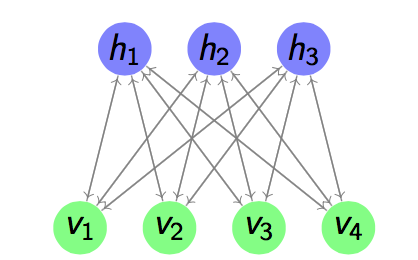
Figure 1.1: A Restricted Boltzmann Machine
The energy function is shown below:
$$E(v,h) = - \sum_{j \in hidden}a_jhj - \sum{i \in visible} b_ivi - \sum{i,j}h_jviw{ij}$$
where $h_j$ $v_i$ represent the value of the hidden and visible units. $a_j$ is the offset of the visible layer and $bi$ is the offsets of the hidden layer. $w{ij}$ is the weights connecting the hidden and visible units. The energy model defines the probability distribution via the energy function:
$$p(\pmb{v,h}) = \frac{1}{Z}e^{-E(\pmb{v,h})}$$
where $Z$ called partition function is a sum of all possible combinations of visible and hidden vectors:
$$Z=\sum_{\pmb{v,h}} e^{-E(\pmb{v,h})}$$
The probability of a given vector can be calculated by summing all hidden units:
$$p(\pmb{v}) = \frac{1}{Z}\sum_{\pmb{h}}e^{-E(\pmb{v,h})}$$
According to the free energy function of Energy-Based Models $G(\pmb{v}) = -\log\sum_{\pmb{h}}e^{-E(\pmb{v,h})}$, we can get the free energy of RBM model:
$$G(v) = - bv - \sum{i} \log\sum{h_i} e^{h_i(a_i + W_i v)}$$
The probability assigned to a training input can be increased via adjusting $W$, $\pmb{a}$ and $\pmb{b}$ to make the energy of the training examples lower and other examples in the input space higher. Both of the visible units $\pmb{v}$ and hidden units are conditionally independent of one anther, by reason of its specific structure. It can be mathematically expressed as:
$$P(h_i = 1|\pmb{v}) = sigmoid(W_i\pmb{v} + a_i)$$
$$P(v_j = 1|\pmb{h}) = sigmoid(W_j\pmb{h} + b_j)$$
Then the free energy of a RBM can be simplified to the following equation:
$$G(\pmb{v}) = -\pmb{bv} -\sum_{i}\log{1 + e^{a_i + W_i\pmb{v}}}$$

Figure 1.2: A Restricted Boltzmann Machine
##Deep Belief Networks
Deep Belief Networks (DBNs)[Hinton06] is a greedy layer-wise form network consists of stacked RBMs, and its hierachical architecture is shown in Figure~\ref{DBN}. It is also a graphical model which learns a multi-layer representation of the training examples.
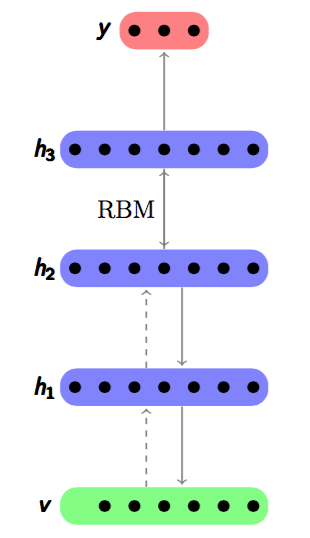
Figure 1.3: A Deep Belief Network
As a stacking autoencoder, an DBN is stacked with RBMs by greedy layer wise unsupervised feature learning[Bengio07] , and each layer is a building block trained by RBM. After the hidden layer $\pmb{h^{i}}$ is trained, in next train step it will be as the visible layer, and the successive layer $h^{i + 1}$ will be the hidden layer. The joint distribution between input $\pmb{x}$ and all hidden layers $\pmb{h^{i}} (i\in [1,n])$ can be expressed in Equation~\ref{joint} below. $n$ is the number of RBM layrs. $x$ is the first layer so it can also be viewed as $\pmb{h^{0}}$. $P(\pmb{h^{n-1},h^{n}})$ is the joint probability between visible layer $\pmb{h^{n-1}}$ and hidden layer $\pmb{h^{n}}$ which is on the top of the DBN. $P(\pmb{h^{i-1}|h^i})$ is the distribution for the visible layer $\pmb{h^{i-1}}$ conditioned on layer $\pmb{h^i}$ at level $i$.
$$P(\pmb{x, h^1,..,h^n}) = P(\pmb{h^{n-1}, h^n})\left(\prod_{i=1}^{n-1}P(\pmb{h^{i-1}|h^{i}})\right)$$
The training process of DBN is shown in Algorithm:

For the fine-tuning part in this project, a logistic regression classifier was extended to the last layer. A training label will be assigned to each input and the parameters of the DBN will be tuned by gradient descent algorithm based on the negative log likelihood cost function.
[Hinton06] Geoffrey E Hinton, Simon Osindero, and Yee-Whye Teh. A fast learning algo- rithm for deep belief nets. Neural computation, 18(7):1527–1554, 2006.
[Mohamed11] Abdel-rahman Mohamed, Tara N Sainath, George Dahl, Bhuvana Ramabhad- ran, Geo↵rey E Hinton, Michael Picheny, et al. Deep belief networks using discriminative features for phone recognition. In Acoustics, Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on, pages 5060– 5063. IEEE, 2011.
[Salakhutdinov07] Ruslan Salakhutdinov, Andriy Mnih, and Geo↵rey Hinton. Restricted boltz- mann machines for collaborative filtering. In Proceedings of the 24th interna- tional conference on Machine learning, pages 791–798. ACM, 2007.
[Hinton10] Geoffrey Hinton. A practical guide to training restricted boltzmann machines. Momentum, 9(1):926, 2010.
[Bengio07] Yoshua Bengio, Pascal Lamblin, Dan Popovici, Hugo Larochelle, et al. Greedy layer-wise training of deep networks. Advances in neural information processing systems, 19:153, 2007.